8.1 Verteilung der Daten

Auf die verschiedenen Darstellungsformen gehen wir noch nicht ein, aber die Verteilung der Daten spielt für statistische Tests eine große Rolle. Sich die Verteilung optisch anzusehen bietet sich durch ein Histogram oder eine Dichteverteilung der Häufigkeiten:

# Als Histogram mit der Anzahl der observations
koog_day %>%
  ggplot(aes(st10)) +
  geom_histogram(bins = 100) # Die Anzahl der bins spiegelt die Klassen wieder. Default sind 30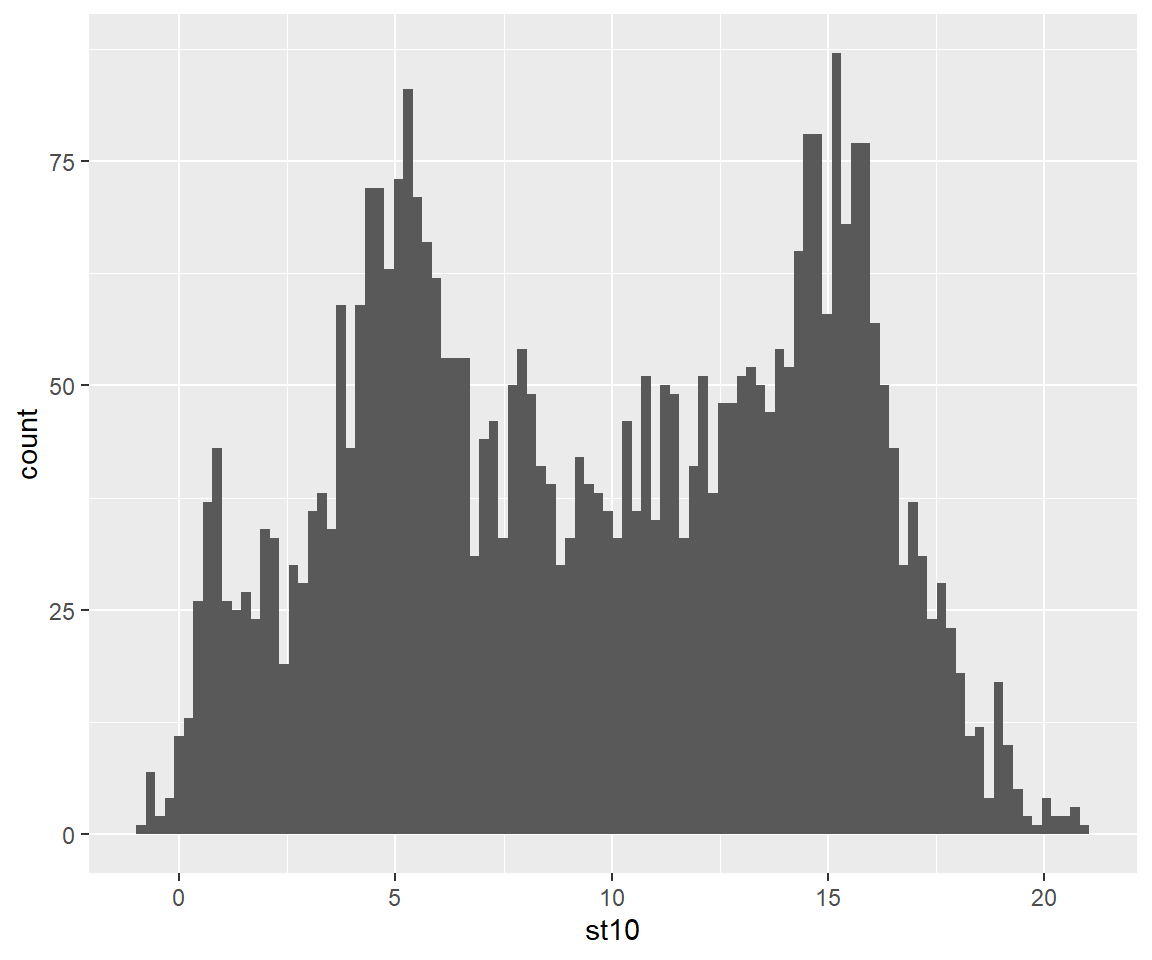 

# Oder als Dichteverteilung
koog_day %>%
  ggplot(aes(st10)) +
  geom_density()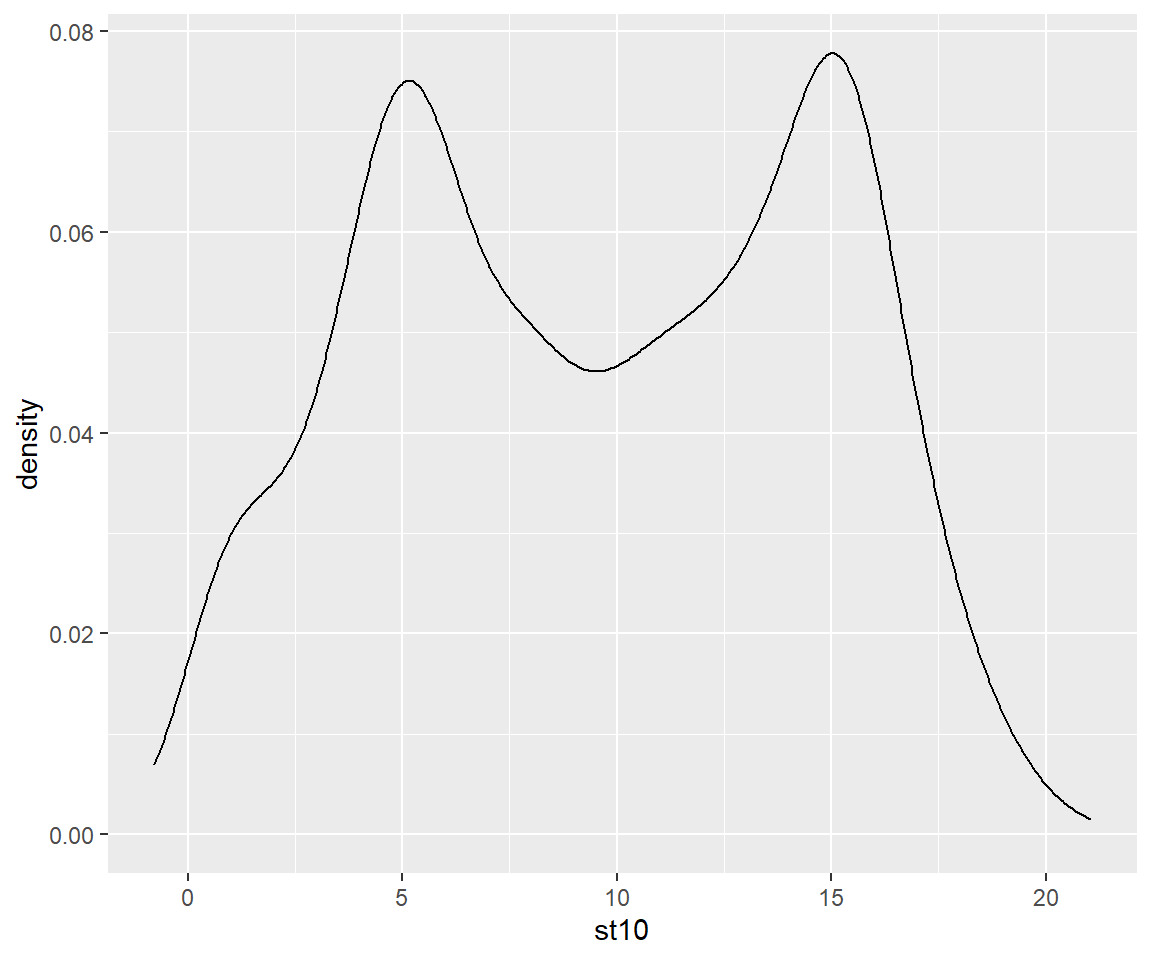

Optisch sieht es nach einer bimodalen Verteilung aus. Statistische Tests wie Korrelation, Regression, t-Test und Varianzanalyse setzen aber eine Normalverteilung voraus. Man nennt diese Tests auch parametrische Tests, da sie von der Verteilung der Daten abhängig sind. Eine reine visuelle Untersuchung ist häufig aber irreführend und sollte daher durch einen Test untermauert werden. Mit dem Shapiro-Wilk Test können wir in R untersuchen, ob die Daten normalverteilt sind.

🚨 Test auf Normalität sind abhängig von der Stichprobengröße. Bei kleiner Stichprobenanzahl wird der Test besser bestanden als bei großer.

Die Null-Hypothese des Test besagt, dass die Probenverteilung normal ist. Ist der Test also signfikant, ist die Verteilung nicht-normalverteilt.

library(rstatix)
rstatix::shapiro_test(koog_day$at)
## # A tibble: 1 x 3
##   variable    statistic  p.value
##   <chr>           <dbl>    <dbl>
## 1 koog_day$at     0.988 7.52e-18

Die Daten der Lufttemperatur sind nicht normalverteilt, da der p Wert signfikant ist (p < 0.001). Wir müssen die Null-Hypothese also zurückweisen. Es gibt aber Möglichkeiten dennoch bestimmte Tests durchzuführen, auch wenn die Daten keine Normalverteilung aufweisen. Das Zauberwort lautet:

💡 Datenfransformation