8.3 Korrelationen

Eine Korrelation gehört zu den weit verbreitesten statistischen Maßen. Die Anwendung muss jedoch mit besonderem Augenmaß erfolgen, andernfalls gibt es auch Fehlerquellen. Eine vermeintliche Korrelation aus einer Population kann auch Zufall sein und muss nicht unbedingt durch das Prinzip Ursache-Wirkung verursacht sein. Daher sollte eine Korrelation immer mit einem Signifikanztest verknüpft werden.

Korrelation beschreiben, wie sich Variablen in Abhängigkeit einer anderen Variable verhalten. Beispielsweise

Bildung und Einkommen
Jahr des Tages und Lufttemperatur
Bierkonsum und Bauchumfang

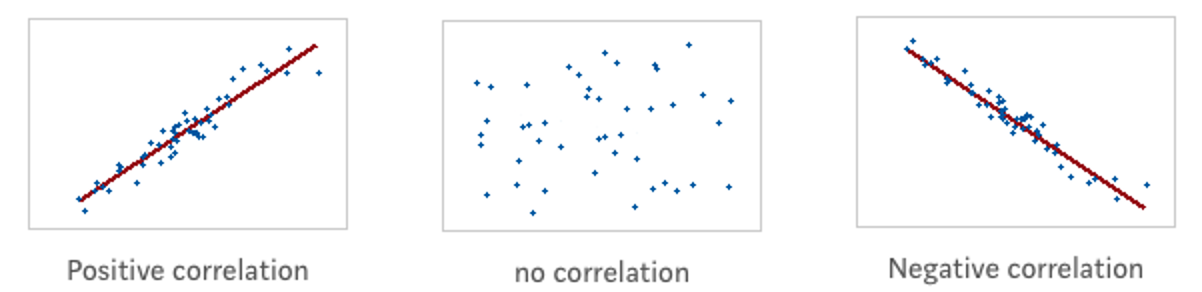
Figure 8.2: Illustration von Z. Jaadi: https://towardsdatascience.com

Positive Korrelation: Zwei Variablen gehen in diesselbe Richtung. Negative Korrelation: Zwei Variablen bewegen sich in gegengesetzte Richtung. Neutrale Korrelation: Es gibt keinen Zusammenhang zwischen den Variablen.

Die Form einer Korrelation kann unterschiedlich ausgeprägt sein:

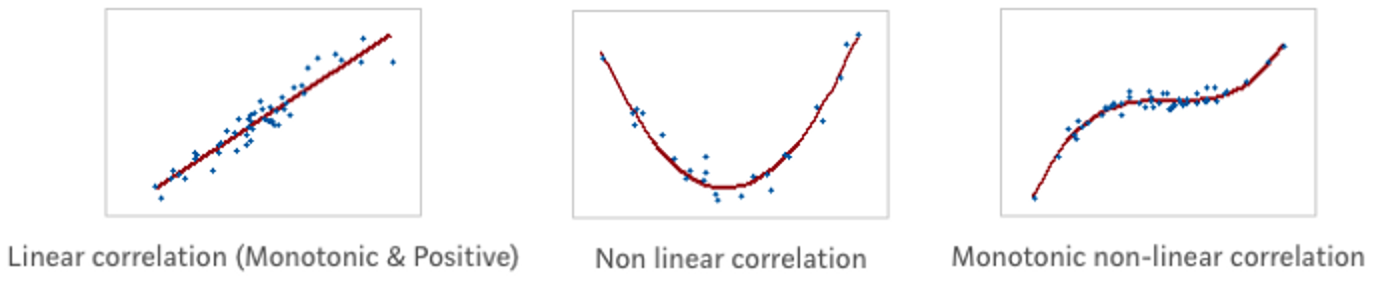
Figure 8.3: Illustration von Z. Jaadi: https://towardsdatascience.com

Lineare Korrelation: Variablen verändern sich in konstanter Rate und erfüllen die Gleichung Y = aX + b (Die Beziehung lässt sich als Gerade beschreiben). Nicht-lineare Korrelation: Variablen verändern sich nicht in konstanter Rate. Die Form kann parabolisch, hyperbolisch, … etc. sein. Monotone Korrelation: Die Variablen tendieren in diesselbe Richtung, jedoch nicht in gleicher Rate. Alle lineare Korrelationen sind also monoton, der umgekehrte Prozess muss jedoch nicht unbedingt richtig sein.

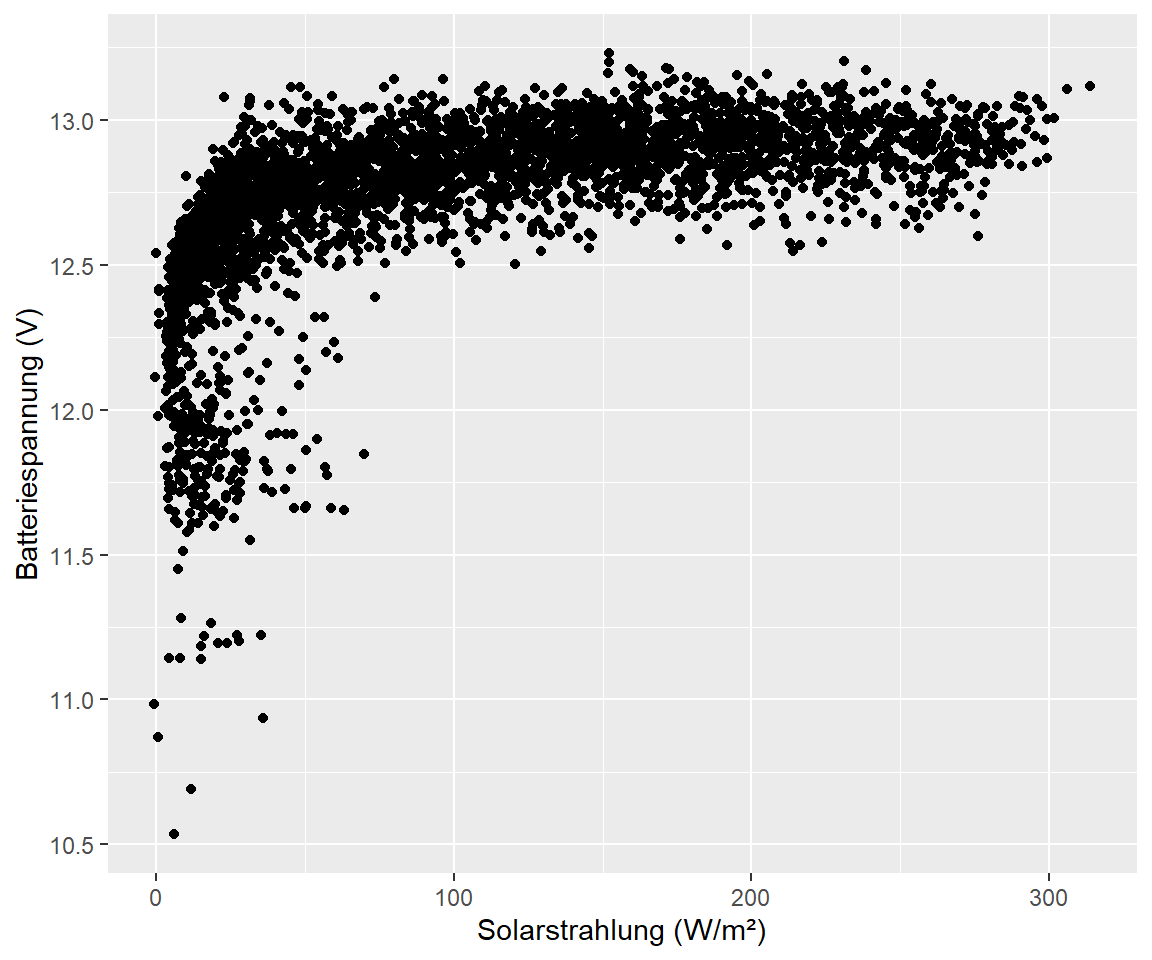
Scatterplots oder Punktdiagramme sind sinnvoll, um visuell einen Überblick über die Verteilung der Daten zu bekommen. Nehmen wir mal das Beispiel Batteriespannung der Station im Speicherkoog und gemessene Solarstrahlung:

koog_day %>%
  ggplot(aes(sr, bat)) +
  geom_point() +
  labs(
    x = "Solarstrahlung (W/m²)",
    y = "Batteriespannung (V)"
  )

8.3.1 Pearson’s Korrelationkoeffizient (r)

Dieses Maß wird verwendet um Stärke und Richtung eines linearen Zusammenhanges zwischen zwei Variablen vorherzusagen. Mathematisch lässt ausgedrückt teilt man die Co-Varianz von zwei Variablen mit dem Produkt der Standardabweichung:

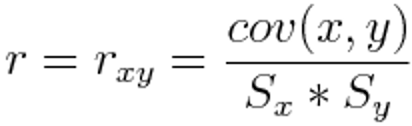
Figure 8.4: Illustration von Z. Jaadi: https://towardsdatascience.com

Die Werte von r variieren zwischen -1 und 1, wobei 1 einen perfekten positiven Zusammenhang darstellt und -1 einen einen perfekten negativen. Die Größe von Pearson’s r könnnte wie folgt eingeteilt werden:

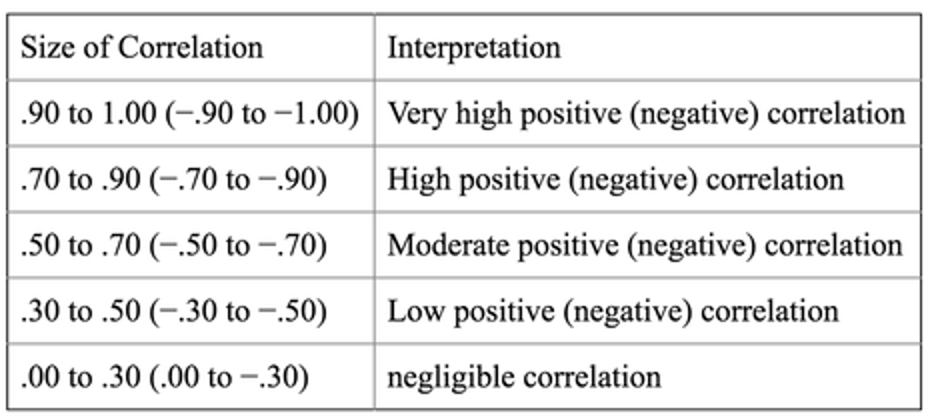
Figure 8.5: Illustration von Z. Jaadi: https://towardsdatascience.com

In R können wir Pearson’s r mit der Funktion stats::cor() berechnen:

cor(koog_day$sr, koog_day$bat, use = "complete.obs", method = "pearson")
## [1] 0.5694954

Mit dem Argument method = können wir die drei Optionen nach Spearman, Pearson oder Kendall’s Tau angeben. Falls wir fehlende Werte in unserem Datensatz haben, was bei uns der Fall ist, dann müssen wir dies im Argument angeben. Wir setzen das Argument complete.obs um Zeilenweise fehlende Werte aus dem Datensatz zu werfen und von der Korrelation auszuschließen.

8.3.2 Signifikanztest

Die Beziehung zwischen zwei Variablen zu quantifizieren ist nur ein Teil der Geschichte. Häufig stellt man Korrelationen zwischen verschiedenen Variablen auf, wobei sich die Population dabei unterscheiden kann. Was wir wollen ist also ein Nachweis, dass unsere Beobachtung innerhalb der Population wahr oder falsch ist, welches wir durch aufstellen einer Testhypothese erreichen.

Formulierung:

Unsere Stichprobe ist n groß mit zwei Variablen x und y
Der Korrelationskoeffizient r ist bekannt und kann berechnet werden
Der Korrelationskoefffizient der Population ρ (Griech. Buchstabe “rho”) zwischen x und y ist unbekannt
Ziel: Wir wollen eine Aussage über ρ anhand von r treffen

Der Hypothesen-Test lässt uns erkennen, ob ρ nah an 0 ist (kein signfikanter linearer Zusammenhang zwischen x und y in der Population) oder signifikant unterschiedlich von 0 (es gibt einen signfikanten linearern Zusammenhang zwischen x und y in der Population).

Schritt 1

Die alternative Hypothese ist immer das, was wir versuchen nachzuweisen (also in unserem Fall das der Zusammenhang signifikant ist mit ρ ≠ 0). Die Null Hypothese versuchen wir zurückzuweisen, also das es keinen signfikanten Zusammenhang gibt mit ρ = 0.

Schritt 2

Wir wenden einen T-Test (auch Student’s T-Test genannt) an um anhang des Stichprobenumfangs n Rückschlüsse über die Gesamte Population zu treffen. Der Wert t des Tests erhalten wir durch:

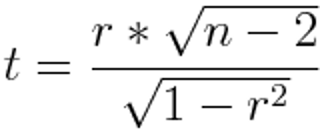
Figure 8.6: Illustration von Z. Jaadi: https://towardsdatascience.com

mit n = Stichprobenumfang und r = Korrelationskoeffizient. Je größer der T-Wert ist, desto wahrscheinlicher ist es das die Korrelation wiederholbar und damit signifikant ist. Aber wie groß ist groß genug? Das ist der nächste Schritt.

Schritt 3

Jeder T-Wert hat einen assoziierten p-Wert. Der p-Wert ist die Wahrscheinlichkeit, dass die Null-Hypothese wahr ist. In unserem Beispiel also die Wahrscheinlichkeit, dass die Korrelation zwischen x und y zufällig ist. Ein p-Wert von 0.05 bedeutet, dass die Wahrscheinlichkeit für eine zufällige Korrelation nur 5% beträgt, ein Wert von 0.01 sogar nur 1%. In den meisten Studien wird die Grenze zwischen signifikant und nicht-signfikant bei einem p-Wert von 0.05 gesetzt oder kleiner. Dieser Bereich ist der Signifikanzbereich α. Wir können unser Signfikanzlevel bei 0.05 setzen (α = 0.05) und den p-Wert finden. Dazu benötigen wir (i) den T-Wert (Schritt 2) und die Anzahl der Freiheitsgrade die berechnet werden können mit df = n - 2. Aus diesen beiden Werten kann der p-Wert mit einer Software oder durch nachschlagen in T-Tabellen erfolgen.

Wenn der p-Wert kleiner als das Signifikanzlevel (α = 0.05) ist, dann wird die Null-Hypothese zurückgewiesen. Die Korrelation ist also statistisch signifkant!
Wenn der p-Wert größer ist, können wir die Null-Hypothese nicht zurückweisen und es gibt keinen signfikanten Zusammenhang zwischen den Variablen.

In R können wir den p-Wert mit der Funktion cor.test() berechnen:

cor.test(koog_day$sr, koog_day$bat, method = "pearson", na.action = "na.omit")
## 
##  Pearson's product-moment correlation
## 
## data:  koog_day$sr and koog_day$bat
## t = 42.641, df = 3788, p-value < 2.2e-16
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
##  0.5475856 0.5906248
## sample estimates:
##       cor 
## 0.5694954

Unser p-Wert ist < 2.2e-16 und damit niedriger als unser Signfikanzlevel bei 0.05 (α = 0.05). Wir können die Null-Hypothese also zurückweisen es gibt einen signfikanten linearen Zusammenhang in unseren Variablen Solarstrahlung und Batteriespannung.

8.3.3 Korrelation vs. Regression

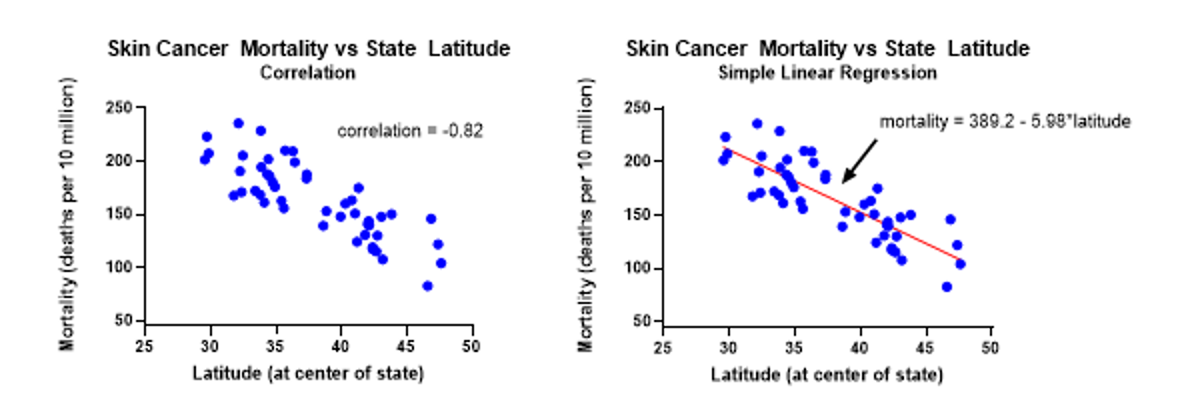
Figure 8.7: Illustration von Z. Jaadi: https://towardsdatascience.com

Diese Begriffe werden häufig durcheinander geworfen. Korrelation ist ein statistisches Maß um die Richtung und Stärke eines Zusammenhanges wiederzugeben. Regression ist eine Technik um die abhängige Variable y vorherzusagen basierend auf der bekannten Variable x und der Gleichung y = a + bx.