8.2 Datentransformation

🔍 Das folgende Kapitel bezieht sich auf datanovia.com

Um parametrische Tests (bspw. t-Test) durchzuführen, müssen die Daten normalverteilt vorliegen. Häufig liegen Daten aber auch links- oder rechtsschief vor.

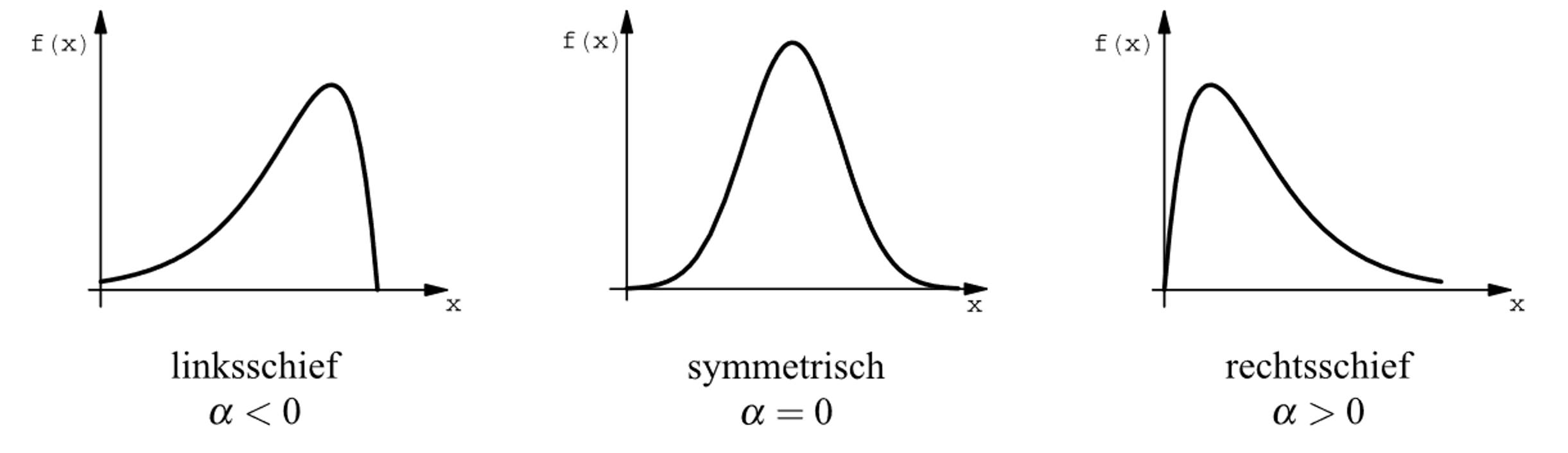
Figure 8.1: Schiefe einer Verteilung

Zuerst wollen wir uns die Dichteverteilung der Daten für die Lufttemperatur im Speicherkoog ansehen. Die rote Kurve spiegelt die perfekte Normalverteilung wieder.

koog_day %>%
  ggdensity(x = "at", fill = "lightgray", title = "Air temperature") +
  stat_overlay_normal_density(color = "red", linetype = "dashed")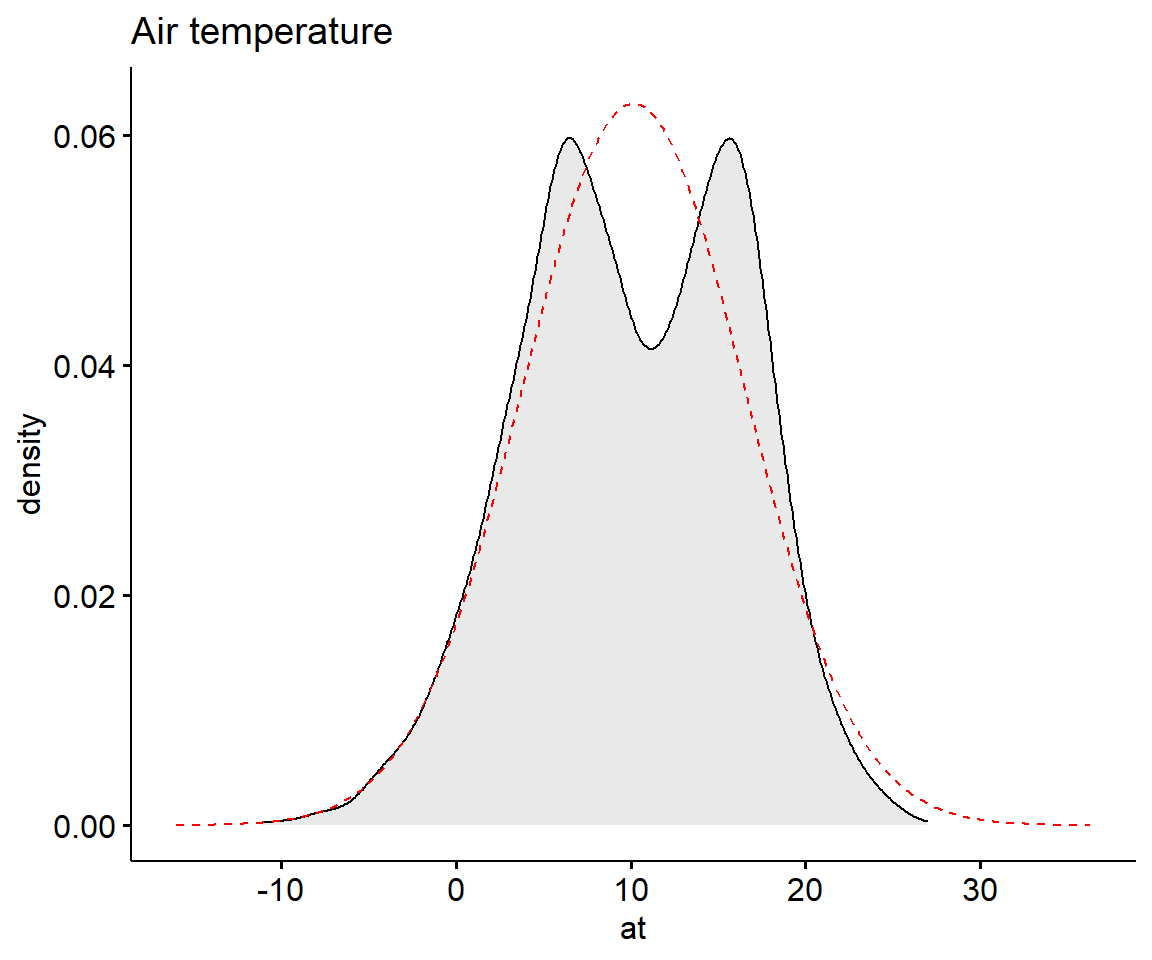

Die Schiefe der Daten kann mit der Funktion skewness aus dem moments:: package analysiert werden. Positive Schiefe (rechtsschief) Median < Mean und Negative Schiefe (linksschief) Median > Mean

skewness(koog_day$at, na.rm = T)
## [1] -0.1630061

• Eine 0 bedeutet keine Schiefe und Normalverteilung
• Negative Werte = negative Schiefe = linksschief
• Positive Werte = positive Schiefe = rechtsschief

Die Daten der Lufttemperatur haben also eine leichte linksschiefe.

Häufig verwendet man eine Log-Transformation der Daten, um eine Normalverteilung zu erreichen. Dazu erstellen wir einen neuen Vektor und nennen ihn at_log

# Quadratwurzel für moderate Schiefe
#at_transform <- sqrt(koog_day$at) # Positive Schiefe
at_transform <- sqrt(max(koog_day$at + 1) - koog_day$at) # Negative Schiefe

# log für stärkere Schiefe
#at_transform <- log10(koog_day$at)
at_transform <- log10(max(koog_day$at+1, na.rm = T) - koog_day$at) 

# Invers für sehr starke Schiefe
at_transform <- 1/koog_day$at
at_transform <- (max(koog_day$at+1) - koog_day$at)


at_transform %>%
  ggdensity(fill = "lightgray", title = "Air temperature") +
  stat_overlay_normal_density(color = "red", linetype = "dashed")

skewness(at_transform, na.rm = T)
## [1] NaN

🚨 Wichtig! Eine Transformation ist nicht immer erfolgreich. In diesem Beispiel hat keine Methode zu einer Verbesserung geführt.

Falls die Normalverteilung nicht gegeben ist und auch die Transformation keine Verbesserung bringt, kann man einen parametrischen Test an der transformierten und der nicht-transfomrierten Variante durchführen. Wenn beide Varianten zu dem selben Ergebniss kommen, ist das Arbeiten mit nicht transformierten Variablen zu bevorzugen. Die Vergelichbarkeit wird bei der Transfomration nämlich schlechter, bspw. bei dem Vergleich von zwei Gruppen kann man nach der Transformation nicht mehr ohne weiteres sagen, dass der Mittelwert von Gruppe 1 > Gruppe 2 ist.

💡 Wenn die Stichprobenanzahl groß genug ist (> 30 - 40), ist die Wahrscheinlichkeit für Normalverteilung meist gegegeben oder zumindest nah genug dran, um mit parametrischen Tests weiterzuarbeiten (Zentraler Grenzwertsatz)